Calculadora de tamaño de muestra
Escribe el margen de error que quieres alcanzar para calcular el tamaño de la muestra que necesitas. En esta página también encontrarás una explicación detallada de los parámetros y las fórmulas que se utilizan para calcular el tamaño de la muestra.
Utiliza la calculadora de margen de error si ya conoces el tamaño de la muestra y necesitas calcular el margen de error.
Tabla de Contenido
- ¿Qué es el margen de error?
- ¿Qué son los intervalos de confianza?
- ¿Qué es la población total o tamaño del universo?
- ¿Qué es el nivel de confianza?
- ¿Qué es la probabilidad de éxito/fracaso?
- Fórmula para calcular el tamaño de la muestra de una población infinita
- Fórmula para calcular el tamaño de la muestra de una población finita
¿Qué es el margen de error?
El margen de error es un porcentaje que define los rangos más probables dentro de los cuales estarán los resultados de tu estudio. Para una muestra de 600 casos con un nivel de confianza de 95% y una probabilidad de éxito/fracaso de 50%, el margen de error es de ±4%. Esto quiere decir que los valores estimados por tu encuesta pueden estar 4% por encima o por debajo de los resultados.
¿Qué son los intervalos de confianza?
A los rangos de valores más probables que se definen con los resultados y el margen de error de tu estudio se les denomina intervalos de confianza.
Por ejemplo, imagina que obtienes una muestra de 600 casos durante una campaña política y encuentras que el candidato que lidera tu encuesta obtiene el 50% de los votos y el que va segundo marca 24%. El margen de error de esta muestra de 600 casos es ±4%. Los intervalos de confianza de los resultados de tu encuesta serían los siguientes.
| Candidato | Intención de voto | Intervalo de confianza |
|---|---|---|
| #1 | 50% | Entre 46% y 54% |
| #2 | 24% | Entre 20% y 28% |
Para este ejemplo es claro que el resultado final no variará si obtienes 1,200 casos para reducir el margen de error a 2.83%: el Candidato #1 seguirá teniendo la misma amplia ventaja. Aumentar el tamaño de la muestra a 1,200 casos sería un completo desperdicio de tiempo y dinero, para este ejemplo.
Sin embargo, si en esta misma muestra de 600 casos los candidatos marcaran 45% y 40% en la preferencia de los votantes, el margen de error continuaría siendo ±4%, pero los intervalos de confianza serían los siguientes.
| Candidato | Intención de voto | Intervalo de confianza |
|---|---|---|
| #1 | 45% | Entre 41% y 49% |
| #2 | 40% | Entre 36% y 44% |
Estos intervalos de confianza se traslapan. En este caso sí sería necesario que aumentes el tamaño de la muestra para disminuir el margen de error, reducir los intervalos de confianza y obtener números que te acerquen más a la verdad.
¿Qué es la población total o tamaño del universo?
La población total y el tamaño del universo son lo mismo. Se refieren a la cantidad total de personas que conforman el grupo que estás estudiando. Este parámetro solo afecta el tamaño de la muestra de manera significativa cuando mides poblaciones pequeñas, de unos pocos cientos o miles de personas. Cuando la población total es grande, de varias decenas o cientos de miles de personas, el tamaño de la muestra varía muy poco o nada a medida que aumenta el tamaño del universo, manteniendo el mismo margen de error.
Veamos un ejemplo y utilicemos la calculadora para entenderlo mejor. Digamos que quieres saber cuál es el tamaño de la muestra que necesitas para hacer un estudio de una comunidad de 1,000 habitantes y obtener un margen de error de 4%. Calcula el tamaño de la muestra introduciendo los siguientes valores en la calculadora de arriba:
- Margen de error: 4%
- Población total: 1,000
- Nivel de confianza: 95%
- Probabilidad de éxito/fracaso: 50%
Necesitarías una muestra de 375 casos para alcanzar el margen de error de 4% que deseas. Pero ¿cuál sería el tamaño de la muestra necesaria para alcanzar el 4% de margen de error si se tratase de una ciudad de un millón de habitantes?
- Margen de error: 4%
- Población total: 1,000,000
- Nivel de confianza: 95%
- Probabilidad de éxito/fracaso: 50%
Ahora el tamaño de la muestra se incrementa y llega a 600 casos para obtener el mismo 4% de margen de error. En la siguiente tabla puedes observar cómo varía el tamaño de la muestra a medida que aumentamos la población total, pero mantenemos el mismo margen de error de 4%.
| Margen de error | Población total | Tamaño de la muestra |
|---|---|---|
| 4% | 1,000 | 375 |
| 4% | 2,000 | 462 |
| 4% | 10,000 | 566 |
| 4% | 50,000 | 593 |
| 4% | 100,000 | 597 |
| 4% | 200,000 | 598 |
| 4% | 400,000 | 599 |
| 4% | 500,000 | 600 |
| 4% | 1,000,0000 | 600 |
Para universos de 500,000 personas o más vemos la misma muestra de 600 casos, y este tamaño no variará si seguimos aumentando la población total. De hecho, para las poblaciones entre 100,000 y 500,000 personas el tamaño de la muestra solo pasa de 597 a 600 casos para obtener el mismo 4% de margen de error, solo 3 casos de diferencia. Esto puede considerarse despreciable tomando en cuenta que estamos hablando de una muestra de 600 casos.
El tamaño del universo solo es relevante cuando hablamos de poblaciones pequeñas. Se hace obvio que, para conocer la opinión de las personas en una comunidad de 1,000 habitantes, necesitaremos menos entrevistas que si se tratase de una ciudad de 1 millón de habitantes, utilizando un mismo margen de error.
Cuando haces estudios electorales, que es el mayor uso de las encuestas telefónicas automáticas, por lo general mides poblaciones de varias decenas o cientos de miles de personas, lo que convierte al tamaño del universo en un parámetro irrelevante. Por este motivo en la calculadora hay una nota que dice: déjalo en blanco si no lo conoces.
¿Qué es el nivel de confianza?
El nivel de confianza indica con qué certeza puedes decir que la realidad está dentro del intervalo que arrojó tu encuesta. Este valor lo verás en algunas fichas técnicas como 1-alfa igual a 90%, 95%, o 99%. El nivel de confianza más utilizado es 95%.
Hagamos un ejercicio para entenderlo mejor. Utilizando la calculadora de arriba obtén el tamaño de la muestra necesario para alcanzar un margen de error de 4%, dejando la población total en blanco, el nivel de confianza en 95%, y la probabilidad de éxito/fracaso en 50%. El tamaño de esta muestra es 600 casos.
Esto significa que si haces una encuesta de 600 entrevistas y los resultados indican que el Candidato Fulano recibiría el 44% de los votos, puesto que el margen de error es ±4%, en realidad estás indicando que los votos estimados que recibirá el Candidato Fulano están entre 40% (44%-4%) y 48% (44%+4%). Este margen de error de 4% lo obtuviste con un nivel de confianza o certeza de 95%, es decir, con un 5% de probabilidades de que la realidad esté fuera del intervalo de confianza que arrojó tu estudio, que es entre 40% y 48%.
Ahora calcula el tamaño de la muestra que necesitarías para alcanzar el mismo 4% de margen de error, pero esta vez con un nivel de confianza de 99%. Encontrarás que tendrías que obtener 1,037 entrevistas para alcanzar el mismo 4% de margen de error. En otras palabras, necesitarías 437 casos adicionales para tener una certeza del 99%, y poder decir que solo existe un 1% de probabilidades de que el Candidato Fulano no reciba entre 40% y 48% de los votos.
¿Qué es la probabilidad de éxito/fracaso?
La probabilidad de éxito/fracaso es un valor aproximado de lo que estás midiendo, y que conoces antes de hacer el estudio. Si tienes una idea de cuál es el valor esperado puedes obtener un mismo margen de error con menos entrevistas.
Por ejemplo, supongamos que estás haciendo un estudio para determinar qué porcentaje de una población votará en las próximas elecciones, y los resultados de varias elecciones anteriores indican que este valor está alrededor del 70%. Si utilizas la calculadora de arriba para obtener el tamaño de la muestra necesario para alcanzar un margen de error de 3% con una probabilidad de éxito/fracaso de 70%, dejando el universo en blanco, y el nivel de confianza en 95%, obtendrás que necesitarías 896 entrevistas.
Si no quieres aventurarte a decir cuál es el valor esperado o no tienes información previa, debes utilizar una probabilidad de éxito/fracaso de 50%, que habrás visto en varias fichas técnicas de encuestas como p = q = 0.5. Cuando utilizas una probabilidad de éxito/fracaso de 50% obtienes el tamaño de la muestra más grande necesario para alcanzar el margen de error que deseas. Siguiendo el ejemplo anterior, con una probabilidad de éxito/fracaso de 50% necesitarías 1,067 entrevistas para llegar al mismo 3% de error.
La mayoría de las veces verás en las fichas técnicas de las encuestas la frase “siendo p = q = 0.5”, lo que simplemente quiere decir “utilizamos el tamaño de la muestra más grande necesario para obtener el margen de error que aquí indicamos”. Rara vez utilizarás una probabilidad de éxito/fracaso distinta al 50%.
Fórmula para calcular el tamaño de la muestra de una población infinita
La siguiente fórmula se utiliza para calcular el tamaño de la muestra de una población infinita, es decir, cuando el tamaño del universo es grande, de varias decenas o cientos de miles de personas.
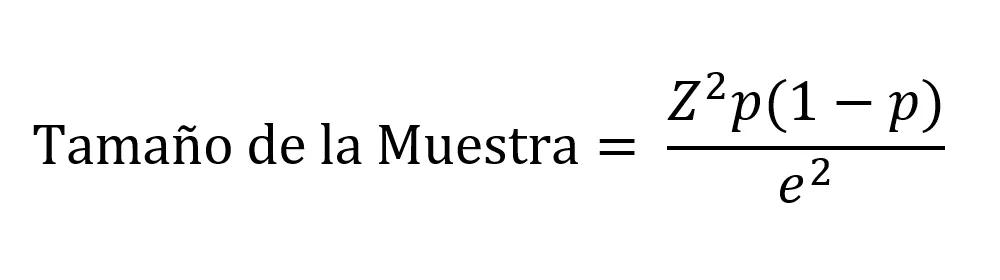
Donde:
- Z es el puntaje Z y depende del nivel de confianza
- p es la probabilidad de éxito/fracaso
- e es el margen de error
Nota: algunas fórmulas reemplazan (1-p) con la letra q. Es por lo que habrás visto p = q = 0.5 en fichas técnicas que indican un 50% de probabilidad de éxito/fracaso.
El puntaje Z depende del nivel de confianza que hayas escogido. La siguiente tabla enumera los puntajes Z correspondientes a algunos niveles de confianza. El 95% es el nivel de confianza más utilizado y su puntaje Z es 1.96.
| Nivel de confianza | Puntaje Z |
|---|---|
| 80% | 1.2816 |
| 85% | 1.4395 |
| 90% | 1.6449 |
| 95% | 1.9600 |
| 96% | 2.0537 |
| 98% | 2.3263 |
| 99% | 2.5758 |
Fórmula para calcular el tamaño de la muestra de una población finita
La siguiente fórmula es la utilizada para calcular el tamaño de la muestra de una población finita, es decir, cuando conoces el tamaño del universo y es pequeño, de unos pocos cientos o miles de personas.
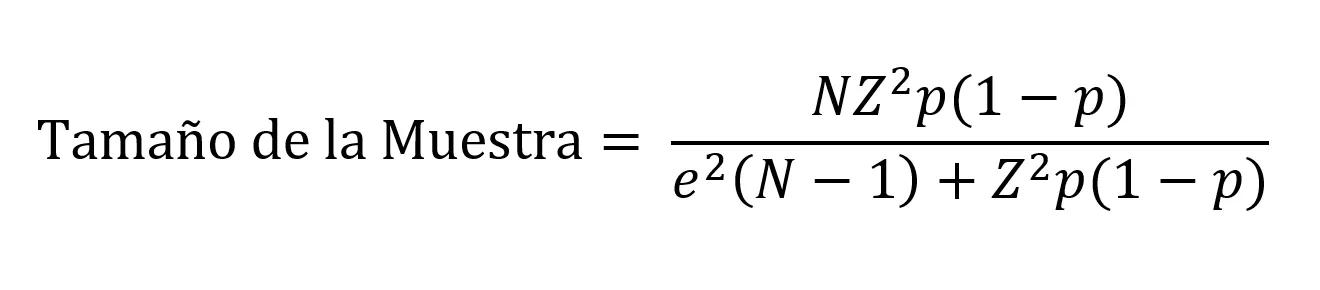
Donde:
- N es el tamaño del universo
- Z es el puntaje Z y depende del nivel de confianza
- p es la probabilidad de éxito/fracaso
- e es el margen de error